A painful tradeoff between a number of infected and negative economic impact must be considered before deciding on the lockdown strategy within a city. As national economies continue to crumble, citizens wonder whether their governments did a good job at regulating the lockdown measures.
Russian city of St. Petersburg is at the frontlines of this ongoing war with Covid-19. To combat this situation effectively, Russian government allocated significant funds for the research. Results followed. Scientists from Peter the Great St.Petersburg Polytechnic University (SPbPU) modified the existing SIR class pandemic prediction model. Now it is better.
But why? What is the nature of this modification? Why is it necessary? And what kind of benefits does this modification provide?
Let's take a look:
Existing SIR (Susceptible - Infected - Recovered) class of models is widely known.
There are many modifications to the SIR model. One of them is SEIR (Susceptible - Exposed - Infected - Recovered)
The SEIR model was taken as a basis and then expanded to include another group: individuals in isolation or quarantine. That was the modification.
But why is this so important? To account for individuals in isolation or quarantine? Let's read the quote from the study:
"This modification of the SEIR model allows the number of susceptible individuals available for infection during modelling to be adjusted according to isolation scenarios (i.e., measures designed to prevent susceptible people from becoming infected). This means the model becomes more accurate, as the reduction of individuals in contact during the pandemic is objectively present in society. Moreover, the modification creates the possibility for scenario modelling. Scenario modelling involves assessing the epidemiological consequences of various strategies for countering the spread of an infectious disease in a given region."
This model has been tested on data from St.Petersburg.
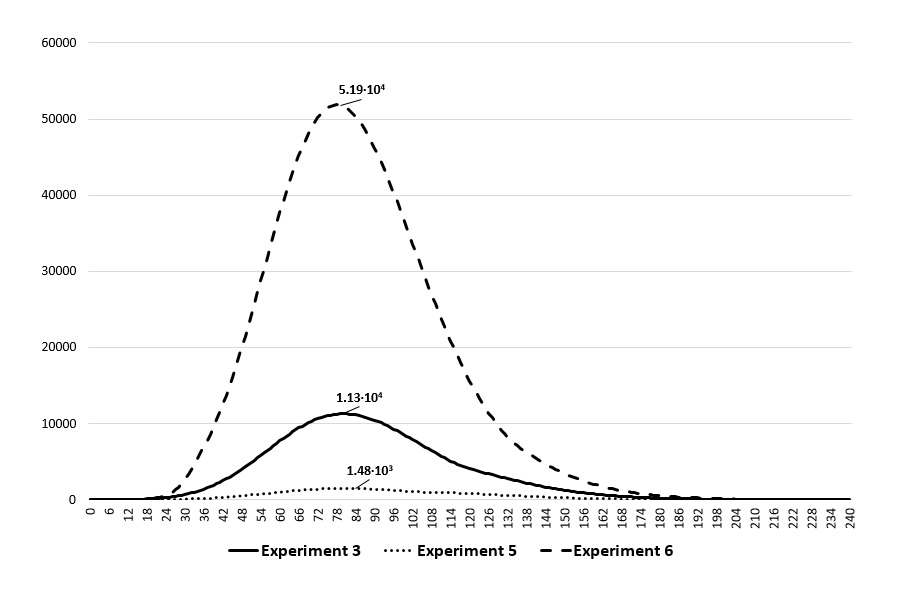
A set of six experiments was sufficient to assess the impact of quarantine measures. The initial data for each experiment include isolated industries that indicate the timing of the introduction and lifting of isolation measures.
The results of this first group demonstrate that the dynamics of the virus' spread have a nonlinear dependence on the number of workers employed in the isolated sectors of the economy. For example, the isolation of three economic sectors, which make up approximately 42% of the total number of workers, reduces the peak number of infected people by 6.2 times and the total number of patients by 4.83 times. Isolation of six sectors of the economy, accounting for 80% of the total number of workers, reduces the peak number of infected people by 75 times and the total number of recovered individuals by 56 times".
The results of the second group show that the introduction of measures to isolate the economy and public life in the early stages of virus' spread can reduce the incidence of the disease and bring an earlier end to the pandemic. Conversely, the late introduction of isolation measures affects the dynamics of the disease's spread to a lesser extent. These results support assessments made by leading epidemiologists. These results indicate that the optimal disease-countering strategy is total isolation as early as possible.
This modified version of the SEIR model can be used to develop strategies for countering the spread of infectious diseases. It also enables researchers to assess the possible mortality in each case as a proportion of the total infected and recovered population.
The article develops a methodological apparatus of a SIR-class model for practical use in decision-making by regional leaders.



.jpg)
.jpg)